Recent News
Letter from the Chair 2023
Feb 19, 2023

Alumni and friends of the Mathematics Department,
There have been a number of changes around here over the last year (quite apart from the upcoming change to semesters, which drives most of our recent faculty meetings). First our Administrative Coordinator Kara Hahlbeck was promoted to personnel analyst which involved a move across the building to the Dean’s office. If you swing by the office now, you’ll meet our new Administrative Coordinator Sabrina Thomas. Sabrina, who graduated from USC with a Bachelor’s degree in biology and Cal State LA with her MBA, comes to us by way of the ONELEGACY company in Los Angeles where she served as donor information coordinator. Together with Melissa Sunata, Sabrina is doing a great job keeping the office running.
Among the faculty we had three professors retire after Spring 2022: Matthew White, Linda Patton, and Marian Robbins all decided to hang up the chalk and are currently enjoying the freedom to pursue other interests. Additionally, Professor Stan Yoshinobu was offered a job at the University of Toronto and elected to make the move official. But don’t worry that our ranks our being depleted. Anticipating these departures, we were able to hire two new faculty members, Sean Gasiorek and Patrick Orson, who started this past Fall are currently in the midst of a search for another math ed specialist to join us in Fall 2023, and expect to pursue an additional hire next academic year. Watch this space for introductions.
The department is also hosting a post-doctorate for the first time ever. Professors Joyce Lin and Elena Dimitrova wrote a successful proposal to the Frost fund to support a two-year position, and invited Warren Roche to join the department in Fall 2022 right after finishing his PhD at the Waterford Institute of Technology in Ireland. Finally, we also hired one new full-time lecturer, Marvin McClendon, by way of a long career starting with a Ph.D. from Princeton, including a full professorship at Savannah College of Art and Design, stops in China and Dubai, and most recently the University of North Georgia.
All these new staff and faculty are helping us maintain the mathematical life and educational mission of the department. As well as active individual research programs, we provide rich coursework, supervise successful student research, and support both faculty and student travel to math conferences. So many of these activities are made possible by the generous donations to the department. These allow us to fund important initiatives that take place outside the classroom. We are incredibly grateful for the flexibility and opportunity provided by your generous gifts.
Please keep in touch and let us know what you’ve been up to. We'd love to see you at the department office if you're ever on campus.
Return to Newsletter
Cal Poly Math Students Win Top Honor in Prestigious International Math Competition
Feb 19, 2023

Photo 1: Cal Poly students Madison Lytle, Trevor Loe and Callan Whitney (from left to right) excelled at the international 2022 Mathematical Contest in Modeling (MCM) competition.
By Nick Wilson
After four days of intense focus that students compared to the feverish energy of a hackathon, a Cal Poly team of three undergraduates emerged from a renowned international math competition as the top U.S. team and honored among the best in the world.
The team of two math majors — Madison Lytle (double majoring in aerospace engineering) and Trevor Loe (double majoring in physics) — and Callan Whitney (aerospace engineering) competed in the February 2022 Mathematical Contest in Modeling (MCM) competition among thousands to tackle the question: “What is the best way for a cyclist to exert their energy over the course of a race?”
Working on little sleep on the Cal Poly campus in the Statistics Department Conference Room in Building 25 — grabbing food and showers when they could between Feb. 16 and Feb. 20, 2022 — they finished among the best in the world in the Consortium for Mathematics and its Applications (COMAP) contest.
The result of their 25-page entry titled “Applying Optimal Control with SQP to Cycling Performance Represented by Constituent Course Elements” was the top U.S. result in their competition category and they finished as a team finalist, earning an Outstanding Award in their problem category, among thousands of international competitors.
“This is the best result for a Cal Poly team in over 20 years,” said Dr. Charles D. Camp, Cal Poly professor of Mathematics and MCM advisor.
This year, the student trio received an award from the Mathematical Association of 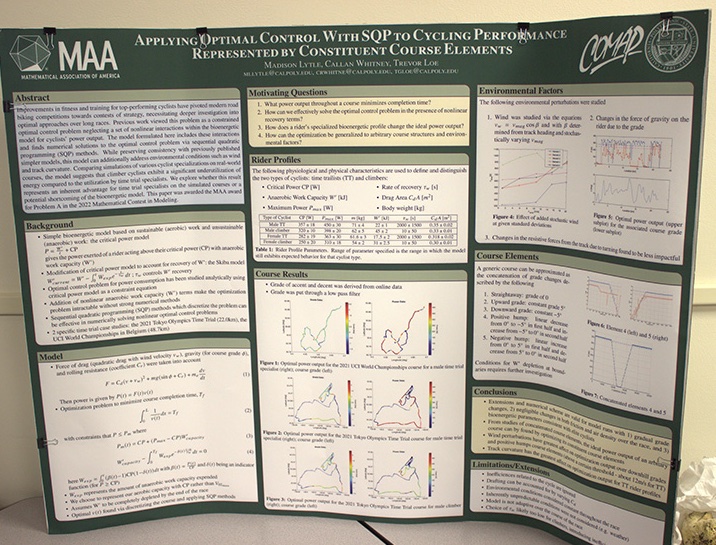 America (MAA) for their outstanding submission, ranking in the Top 29 of approximately 15,000 teams that participated in the competition overall.
America (MAA) for their outstanding submission, ranking in the Top 29 of approximately 15,000 teams that participated in the competition overall.
The Cal Poly team competed in a real-world modeling challenge among MAA college-level peers from across the U.S. and a host of other countries (the other top-ranking teams in their category were from China).
The Cal Poly math competition team displays their poster at the Fall Math Symposium.
Not only was the Cal Poly group’s submission a finalist, a level only 2% of submissions achieved, but their report was chosen by the MAA as the best submission for their problem.
“Their work demonstrated creativity and a deep understanding of the modeling process via their formulation, implementation and analysis of a mathematical model that addressed the given contest question.”
Camp noted that in the year 2000 when a Cal Poly team won an award for an outstanding entry, the competition had 496 teams overall, signifying the elevated competitiveness of the event now.
To determine the optimal energy output of a professional cyclist, the Cal Poly student team considered several variables such as human biology (anaerobic biology), uphill versus downhill grades, drag, and race-track conditions such as curvature and course topography.
Modern power monitoring systems can be mounted on a bike allow riders to track their power output during the race and make informed adjustments about improving pacing.
The group’s analysis laid out formulas, models and conclusions about optimal cycling power output to accomplish the fastest possible results in professional races.
“Madison and I are both are into a lot of applied math work going on at Cal Poly,” said Loe, a double major in physics. “We were able to get a sense of what using the math that we’ve learned feels like.”
Because of variables such as a cyclist’s biological makeup and ability to store energy, along with course conditions such as hills and headwinds, they used sequential quadratic programming (SQP), a mathematical method used to solve a sequence of optimization subproblems, to generate numerical solutions.
They proposed a method of optimizing cycling power output over subsections of tracks, called course elements, that may be concatenated (linked in a chain or series) into complex tracks.
“Whatever parameters you use to represent the rider’s specific biology, there are certain interactions that are nonlinear,” said Lytle, a double major in aerospace engineering. “And that basically just makes them a lot more difficult to optimize and deal with numerically.”
The study involved assessments of three tracks — the Tokyo Olympic Time Trial course, the UCI World Championships in Belgium and a constructed square course consisting of four rises and falls with a mathematically imposed radius of curvature of 10 meters around each bend.
“The objective was not necessarily the model output, but the fact that the model is going to work,” Lytle said. “That’s so we can take into account these anaerobic effects because we can implement them in the model.”
Among their conclusions:
- the optimal strategy involves operating close to max power above one’s critical power (or highest average power you can sustain) during steep inclines, and dropping power output down as much as possible during downhills to recover
- for courses with more variation in grade, model outputs recommend operating more reactively to the course features; alternatively, a flatter course prompts a pace which stays close to critical power at all times
- due consideration should be taken into the environmental “perturbations” of the course, chiefly a strong headwind and the locations of sharp turns. If a headwind is greater than 15 meters per second, model outputs indicate that changing power output reactively to the wind, rather than staying consistent, will lower track times.
The students were not allowed any faculty guidance during the competition.
“Surprisingly, some of my physics classes were really helpful for some of the math, specifically optimization, which some physics classes, especially like classical mechanics, use,” Loe said.
Lytle echoed her teammates assessment that skill sets in multiple disciplines helped.
“Trevor and I are both double majors and Callan is an aerospace engineering major,” Lytle said. “We’ve learned a lot about drag in aerospace engineering classes.”
Loe added: “With this competition, one of the hardest parts is deciding basically infinite things that you could account for and what to include and what to ignore. It was fun and a great experience to use math to solve a real-world problem.”
Return to Newsletter
Polymath 2023
Feb 19, 2023
Featured Articles
Math Stars Excel
Learn about how three Cal Poly students earned the best result out of any United States team in their problem category at an international math competition.
Letter from the Chair
Chair Ben Richert shares updates on new staff members in the department and thanks donors for generous support of programs."
Meet the New Team
Meet new math team members Sabrina Thomas, Warren Roche, Patrick Orson and Sean Gasiorek."
Making their Mark with Grants and Publications
Check out the list of new math grants and publications.
Bringing Cal Poly Math to World
Cal Poly faculty offered workshops on campus and tripped globally for talks, making for an eventful year.
All in a Day's Work - Research and Publications
Apr 6, 2022
 Scholarly activity in the Mathematics Department kept going strong whether remote or in-person. Students and faculty achieved a great deal during the past year.
Scholarly activity in the Mathematics Department kept going strong whether remote or in-person. Students and faculty achieved a great deal during the past year.
Frost Summer Undergraduate Research Program
Ryan Tully-Doyle conducted research with Jackie Driscoll and Justin Hexem on the iteration of complex functions on matrices.
Linda Patton worked with Mav Lara and Brooke Randell on "Characterizing the Numerical Range of Block Toeplitz Operators." They described the numerical ranges of some block Toeplitz operators with symbols of the form F(z)=A+Bz, where A and B are two by two matrices. This required analyzing the convex hull of an infinite collection of ellipses. Their poster was accepted to present at the Joint Mathematics Meeting, which was postponed but will be held virtually in April.
Linda Patton also worked with Kelsey Lowrey, Tim Royston, and Karl Zieber studying "Flat Portions on Numerical Ranges of Nilpotent Matrices." They worked to generalize a conjecture about the maximum number of such flat portions to bigger matrices.
Joyce Lin worked with Aidan Chandrasekaran and Srirag Vuppala on simulating a mean-field equation for the electrical activity in cardiac tissue, as well as with Brady Berg and Joseph Mcguire (jointly supervised with Elena Dimitrova) on creating an agent-based model for cardiac tissue.
Stathis Charalampidis worked with Cal Poly ugraduates: Andy Chiv, Riley Prendergast, and Alexis Saucerman on the project titled "Computation of matter waves in atomic physics."
Elena Dimitrova worked on Topological Data Analysis for Comparison of Simulated and Experimental Images with students Laura Bialozynski, Jaxon Green, Vanessa Newsome-Slade, and Stephen Wessel; in collaboration with Paul Anderson from CS.
Workshops
Professors Elsa Medina and Amélie Schinck-Mikel offered the annual Cal Poly Math Academy in summer 2021. Because of the pandemic, the academy met virtually. Backpacks were sent to each participant's house filled with math manipulatives and fun goodies, providing a hands-on experience even in the remote environment. Every summer the academy employs two Cal Poly undergraduate students who are studying to become secondary mathematics teachers to assist in creating activities and running the sessions.
Medina and Schinck-Mikel plan to bring the Math Academy back in-person for summer 2022. The academy is offered in partnership with the Migrant Education Program for the region.
Publications
E.G. Charalampidis, F. Cooper, J. Dawson, A. Khare and A. Saxena. “Behavior of solitary waves of coupled nonlinear Schrodinger equations subjected to complex external periodic potentials with odd-PT symmetry.” J. Phys. A: Math. and Theor. 54, 145701 (2021)
E.G. Charalampidis, F. Cooper, A. Khare, J. Dawson and A. Saxena. “Stability of trapped solutions of a nonlinear Schrodinger equation with a nonlocal nonlinear self-interaction potential.” J. Phys. A: Math. and Theor. 55, 015703 (2021)
E.G. Charalampidis and V.M. Hur. “Numerical bifurcation and stability for the capillary-gravity Whitham equation.” Wave Motion. 106, 102793 (2021)
C. Chong, Y. Wang, D. Marechal, E.G. Charalampidis, M. Moleron, A.J. Martinez, M.A. Porter, P.G. Kevrekidis and C. Daraio. “Nonlinear Localized Modes in Two-Dimensional Hexagonally-Packed Magnetic Lattices.” New J. Phys. 23, 043008 (2021)
M. Cox, W. Grewe, G. Hochrien, L. Patton, and I. Spitkovsky. “Nonparallel flat portions on the boundaries of numerical ranges of 4-by-4 nilpotent matrices.” Electronic Journal of Linear Algebra. 37 (2021), 504-523
E. Dimitrova, J. Hu, Q. Liang, B. Stigler, A. Zhang. “Algebraic Model Selection and Experimental Design in Biological Data Science.” Advances in Applied Mathematics. 133, 102282 (2022)
T.A. Grundmeier, D. Retsek, A. Berg, S. Mann, A. Hamlin-Prieto. “Assumption and Defintion Use in an Inquiry-Based Introduction to Proof Course.” PRIMUS. 32(1) (2022) 1-13.
G. Kato and K. Nishimura. “Time and Mnemonic Morphism.” Constructive Destruction to Destructive Construction, edited by K. Nishimura, M. Murase, and K. Yoshimura. Springer, October, 2021.
D. R. King, M. Entz 2nd, G. A. Blair, I. Crandell, A. L. Hanlon, J. Lin, G. S. Hoeker, and S. Poelzing. “The conduction velocity-potassium relationship in the heart is modulated by sodium and calcium.” Pflugers Arch. Mar; 473(3) (2021): 557-571. doi: 10.1007/s00424- 021-02537-y. Epub 2021 Mar 4. PMID: 33660028; PMCID: PMC7940307.
S. Koshy-Chenthittayil, E. Dimitrova, E. W. Jenkins, and B. C. Dean. “A Computational Framework for Finding Parameter Sets Associated with Chaotic Dynamics.” In Silico Biology. 14 (1-2) (2021) 41-51
D. Murrugarra and E. Dimitrova. “Quantifying the total effect of edge interventions in discrete multistate networks.” Automatica. 125, 109453 (2021)
F. Ruz, B. Chance, E. Medina, and J. Contreras. “Content Knowledge and Attitudes Towards Stochastics and Its Teaching in Pre-service Chilean Mathematics Teachers.” Statistics Education Research Journal. 20(1) (2021)
A.S. Von der Heydt, P. Ashwin, C.D. Camp, M. Crucifix, H.A. Dijkstra, P. Ditlevsen, and T.M. Lenton. “Quantification and interpretation of the climate variability record.” Global and Planetary Change 197, 103399 (2021)
W. Wang, L.-C. Zhao, E.G. Charalampidis and P.G. Kevrekidis. “Dark-dark soliton breathing patterns in multi-component Bose-Einstein condensates.” J. Phys. B: At. Mol. Opt. Phys. 54, 055301 (2021)
H. Yasuda, E.G. Charalampidis, P.K. Purohit, P.G. Kevrekidis and J.R. Raney. “Wave manipulation using a bistable chain with reversible impurities.” Phys. Rev. E 104, 054209 (2021)
T.D. Todorov, “Infinite-Dimensional Linear Algebra and Solvability of Partial Differential Equations,” Journal of Logic & Analysis (ISSN:1759-9008), 13:5 (2021), p.1-34, (http://arxiv.org/abs/2106.04039), DOI: https://doi.org/10.4115/jla.2021.13.5.
Conferences
Elena Dimitrova gave conference talks at:
-
SIAM Conference on Applied Algebraic Geometry, invited talk, “Algebraic design of experiments for regulatory network identification.” Virtual. August 2021.
-
Society for Mathematical Biology Annual Meeting, invited talk, “Revealing the canalizing structure of Boolean functions – algorithms and applications.” Virtual. June 2021.
Ryan Tully-Doyle gave conference talks at:
-
International Workshop in Operator Theory and its Applications at Chapman University, August 2021.
-
International Workshop in Operator Theory and its Applications at Lancaster University (virtual), August 2021.
-
Focus Program in Noncommutative Function Theory, Fields Institute, November 2021.
Elsa Medina gave conference talks:
-
National Council of Teachers of Mathematics Fall Virtual Conference titled: “How Random is That?” Nov. 2021.
-
Teach Bilingual Learning Summit (virtual), titled: “Ideas for Making Mathematics More Accessible for Students from Diverse Backgrounds” in April 2021.
Students Say It's 'Absolutely Amazing to Be Back in Person'
Apr 6, 2022
 Fall 2021 brought a return to in-person classes. Department club presidents reflect on the positive effects for the community of math majors.
Fall 2021 brought a return to in-person classes. Department club presidents reflect on the positive effects for the community of math majors.
Trinity Kobielusz, Math Club President
“It has been absolutely amazing to be back in person because it has allowed me to reconnect with old friends and also make new friends. I have enjoyed not sitting in front of a computer for all hours of the day and actually being able to talk to my peers in my classes. My level of stress has decreased, and I have been able to manage my time better. Attendance has significantly increased for Math Club since coming back in person. Everyone is eager to be involved and excited to come to our meetings.”
Adrienne Boone, Association for Women in Mathematics Club President
“I switched to the math major during the online spring 2020 quarter. As a result, my classes last year were filled with virtual strangers, so the absolute best part of being back has been getting to know the people outside of the computer! I’ve been able to do things I love with people who I love being around. Whether we’re having fun at the beach or stressing out in the math lounge, I don’t take any of it for granted anymore.
I am especially proud that the Association for Women in Mathematics Club has fostered such a supportive and welcoming environment despite the limitations of the pandemic. Running the club with four other amazing women has solidified my confidence and my love for mathematics. Our bi-weekly meetings and various events have introduced our members to inspiring speakers and provided a space for math-loving people of all identities and backgrounds to feel celebrated and heard. I am so grateful for the community I’ve found in mathematics, and I’m so excited for that community to grow next year.”
Networking and Career Opportunities

The return to campus also gave students unique opportunities to network and seek career advice from local companies. On Dec 1, the operations coordinator, Danielle Borelli, and a recent graduate from the California Cybersecurity institute came to visit. In January, the two Directors, Kim O’Neill and Dmytro Marushkevych, from the Data Science & Analytics Group of Razorfish came to give a talk to the math majors.
Return to Newsletter
Passing on the Favor in Gratitude to Charlie Hanks
Apr 6, 2022

Math alumnus Stephen Corcoran, above, and former Department
Chair Charles Hanks both served in the Coast Guard.
As Stephen Corcoran (Mathematics, B.S., ‘69; M.A., ‘75) tells the story, Charles Hanks was a strong presence in the Cal Poly Mathematics Department. He also played a significant role in Corcoran’s life beyond Cal Poly.
Corcoran came to Cal Poly as an aeronautical engineering major. All engineers took the same two-year calculus progression ending with Hanks’ differential equations course, MATH 318. Along the way, Corcoran also took linear algebra just for fun, and it hooked him on mathematics. He never looked back, not even to tell the Aeronautical Engineering Department that he was changing majors.
“The deeper I got into mathematics, the more I enjoyed it,” Corcoran said.
Though Corcoran didn’t use much math in his 26-year career in the Coast Guard — except for programming in COBOL when he improved the payroll system that paid reservists — Hanks, who was a captain in the Coast Guard Reserve, still influenced Corcoran’s career considerably.
Corcoran joined the Coast Guard directly after graduation, then left in 1974 and decided to return to Cal Poly to pursue his master’s degree. To enroll, he needed approvals from the dean of the college and the Mathematics Department chair, which at the time was Hanks. When Corcoran presented himself, Hanks chewed him out for leaving the Coast Guard, approved his admission and offered him a job teaching agricultural mathematics.
“Better than that, it just doesn’t get,” Corcoran said.
Corcoran finished his master’s degree and began working for the Burroughs Corporation selling computer systems to financial institutions in San Francisco. He often saw Captain Hanks, who came to the Bay Area for his weekend reserve duty.
One weekend Hanks told Corcoran, “Make something out of your life, Corcoran. Go back in the Coast Guard.”
Corcoran told him, “I applied and was rejected. I was just one of too many lieutenants with sea service seeking recall.”
Captain Hanks said, “Try again.” When he reapplied, the Coast Guard found it needed Corcoran. He suspected Hanks had something to do with their change of opinion.
This close relationship between faculty and students and the down-to-earth practicality that Hanks embodied define the Cal Poly experience for Corcoran.
“The professors have their feet on the ground and make things real life,” Corcoran said. “We never had 300 students in an amphitheater class. To the extent possible, the Mathematics Department added enough sections to satisfy the need. If seats were needed for 300 students, somehow the department opened 10 sections. The students got the attention they deserved.”
When Corcoran attended Cal Poly, state funding for higher education was substantial, and college was the free education California was promising. Full-time tuition was $45 for fall quarter and $15 for spring. The difference was a sports fee for fall. Seeing how much state funding has decreased, he wanted to help students today who face much higher tuition costs.
“It’s no longer an education for all situation in California,” Corcoran said.
When Corcoran learned of the Hanks Scholarship, he decided to change his annual contribution from a general contribution to the Mathematics Department to one Hanks Scholarship each year.
“It felt more satisfying to contribute to a particular individual,” Corcoran said. “It’s important to fund the Mathematics Department because of its foundational nature: the department supports the whole university, but there aren’t enough mathematics graduates to make as significant a financial impact as would be desirable. I decided if I could directly help one student, I would better appreciate the impact of my contribution.
“When it came down to putting numbers on paper, I decided to change it to two scholarships and perhaps pleasantly surprise someone. I did not know then that Dr. Hanks’ widow Marjorie had passed and the Mathematics Department was concerned for the future of the Hanks Scholarship. For the next five years at least, we will have two scholarships in Charlie Hanks’ name.”
Hanks’ generosity continues to inspire Corcoran.
“Charlie helped me along the way, likely more than I can know,” he said. “Perhaps I can continue the favor in his name and spirit.”
Supporting Mathematics Students
If you'd like to support mathematics students with a scholarship or a gift to the department, you can contact Morgen Marshall, senior director for advancement and external relations, or make a financial donation.
Return to Newsletter
Letter from the Chair 2022
Apr 5, 2022
 Alumni and friends of the Mathematics Department
Alumni and friends of the Mathematics Department
We’re back in the classroom! It’s been a while since that fateful day when everything went virtual, but the chalk dust is once again flying in building 38. I’m pleased to report that as of winter 2022, math courses are entirely face-to-face.
While math faculty have all become semi-expert with Zoom and other web-based content delivery methods, the main lesson we’ve learned is that online instruction is a poor substitute for good, old-fashioned, face-to-face coursework.
During the virtual experiment that COVID forced upon us, in-person courses were limited to labs and other activity-based experiences, so it wasn’t until fall 2021 that we were first allowed to return to the chalkboards. We are now near the forefront of Cal Poly departments for in-person offerings and frequently get thanked by students for going live.
The beginning of the winter quarter was difficult as each math instructor managed multiple instances of COVID-related student absences. It undoubtedly would have been easier to simply teach the quarter online, so it is a testament to the faculty’s dedication to the live Cal Poly experience that we did the extra work needed to keep our classes in the classroom.
By the time of this writing, things have stabilized nicely. All our usual activities are up and running: the undergraduate study lounge has reopened, students and faculty are traveling to research conferences, our student clubs are back in person, and we’re all looking forward to the math awards banquet and the faculty/student softball game. Hopefully spring quarter will be even smoother.
Finally, we recently conducted a search for two new tenure-track faculty members. This search, chaired by Vince Bonini was fantastically successful, and we are happy to announce that Patrick Orson and Cal Poly alumnus Sean Gasiorak will join us in the fall. Watch this space for official introductions upon their arrival next academic year.
In closing, I'd like to once again thank everyone who has supported the department financially. Your gifts have a direct impact on the quality of our program, funding many of the initiatives which are so important to the major but take place outside the classroom. We are incredibly grateful for the flexibility and opportunity provided by your generous donations.
Please keep in touch and let us know what you’ve been up to. I’m happy to once again be able to say that we'd love to see you at the department office if you're ever on campus.
Return to Newsletter
Math Professor Leads Cal Poly Chapter of Statewide Service Program
Apr 5, 2022

Cal Poly has been selected as one of 45 higher education institutions to implement the statewide #CaliforniansForAll College Corps program on its campus, and math Professor Erin Pearse is helping lead the campus effort.
#CaliforniansForAll College Corps is an initiative by Gov. Gavin Newsom that aims to provide 6,500 college students statewide with service-learning opportunities over the span of two academic years to tackle challenges in climate action, K-12 education and food insecurity.
Thanks to partnerships built by Pearse through the Initiative for Climate Leadership and Resilience, students across campus will have the opportunity to work on climate action projects with community organizations. In true Learn by Doing fashion, students will plan and build the infrastructure that will reduce the carbon footprint of Central Coast communities from Santa Barbara to Santa Cruz.
College of Science and Mathematics media intern Devan Spiegel got all the details from Pearse in a recent episode of the Cal Poly Can podcast. Listen in and find out how students will become climate leaders and receive $10,000 toward their college education in return.
 Listen In
Listen In
Mathematics Professor Erin Pearse talks with media intern Devan Spiegel about #CaliforniansForAll and how Cal Poly students can earn $10,000 for their education while becoming climate leaders in the latest episode of the Cal Poly Can podcast.
Return to Newsletter
Polymath 2022
Apr 5, 2022
Featured Articles
Math Professor Leads Cal Poly Chapter of Statewide Service Program
Through the statewide #CaliforniansForAll College Corps, Cal Poly students will earn $10,000 toward their education by becoming climate leaders, and Math Professor Erin Pearse is leading the way.
Letter from the Chair
Ben Richert celebrates the return to campus and other department achievements.
Students Say It's 'Absolutely Amazing to Be Back in Person'
Club presidents share their experience of being back on campus.
Passing on the Favor in Gratitude to Charlie Hanks
Former department chair Charles Hanks played a significant role in Stephen Corcoran's (Mathematics, B.S., ‘69; M.A., ‘75) life. Now Corcoran has taken over funding a scholarship in Hanks' name.
All in a Day's Work - Research and Publications
From numerical bifurcation, to equations describing electrical activity in cardiac tissue, to hands-on math education manipulatives, students and faculty have been busy.
Letter from the Chair 2021
Apr 7, 2021
 Alumni and friends of the Mathematics Department,
Alumni and friends of the Mathematics Department,
What a year it’s been! Ever since that fateful day in March 2020, all math classes have been conducted as virtual affairs. The change was rather abrupt and could have been a disaster but for the flexibility and ingenuity of math faculty and staff. We recognized right away that nothing can replace the collaborative face-to-face experience that is the centerpiece of our major. It required an incredible effort and sacrifice to reproduce our usual practices as much as possible online — but we rose to the challenge.
While we eagerly await a return to the chalkboards in Building 38, our pandemic operations have made me nothing but proud. Similar observations can be made about our students. Community building and the benefits of peer-to-peer instruction and collaboration — not to mention the encouragement of shared experiences — are difficult to manufacture over Zoom, but math majors are finding a way. Our students have certainly justified our high opinion of their abilities.
The usual activities in the department continue apace though modified by the pandemic. For example, honors during our Spring 2020 Awards Ceremony, usually a banquet, were conferred by many celebrity guests from within and beyond the department, including a special congratulatory shoutout from math Ph.D. Winnie Cooper. We had 25 students and seven faculty members participate in summer research projects with virtual meetings and presentations and I see many interesting senior projects and master’s theses come across my desk digitally. Faculty members' individual research projects also continue. Again, though constrained by circumstances, the department has performed admirably.
A big issue on (virtual) campus lately has been growing Cal Poly’s leadership as a data science and analytics innovator in research and education. The Math Department is part of this campus-wide effort and recently submitted a $1.3 million dollar grant proposal to the National Science Foundation to support data science course development. We look forward to what will happen next with this important undertaking.
Finally, I'd like to once again thank everyone who has supported the department financially. Your gifts have a direct impact on the quality of our program. For example, Math 351 Typesetting with LaTeX; Math 370 Putnam Exam Seminar; and Math 371 Math Modelling Seminar are important classes for the major but cannot be funded via the state budget in 2021-22. Thanks to donor support, though, we will still be able to run these classes next year. We are incredibly grateful for the flexibility and opportunity provided by your generous donations.
Please keep in touch and let us know what you’ve been up to. Once we're all back and live, we'd love to see you at the department office if you're ever on campus.