Cal Poly Math Students Win Top Honor in Prestigious International Math Competition

Photo 1: Cal Poly students Madison Lytle, Trevor Loe and Callan Whitney (from left to right) excelled at the international 2022 Mathematical Contest in Modeling (MCM) competition.

By Nick Wilson

 

After four days of intense focus that students compared to the feverish energy of a hackathon, a Cal Poly team of three undergraduates emerged from a renowned international math competition as the top U.S. team and honored among the best in the world.  

The team of two math majors — Madison Lytle (double majoring in aerospace engineering) and Trevor Loe (double majoring in physics) — and Callan Whitney (aerospace engineering) competed in the February 2022 Mathematical Contest in Modeling (MCM) competition among thousands to tackle the question: “What is the best way for a cyclist to exert their energy over the course of a race?” 

Working on little sleep on the Cal Poly campus in the Statistics Department Conference Room in Building 25 — grabbing food and showers when they could between Feb. 16 and Feb. 20, 2022 — they finished among the best in the world in the Consortium for Mathematics and its Applications (COMAP) contest. 

The result of their 25-page entry titled “Applying Optimal Control with SQP to Cycling Performance Represented by Constituent Course Elements” was the top U.S. result in their competition category and they finished as a team finalist, earning an Outstanding Award in their problem category, among thousands of international competitors.

“This is the best result for a Cal Poly team in over 20 years,” said Dr. Charles D. Camp, Cal Poly professor of Mathematics and MCM advisor.

This year, the student trio received an award from the Mathematical Association of 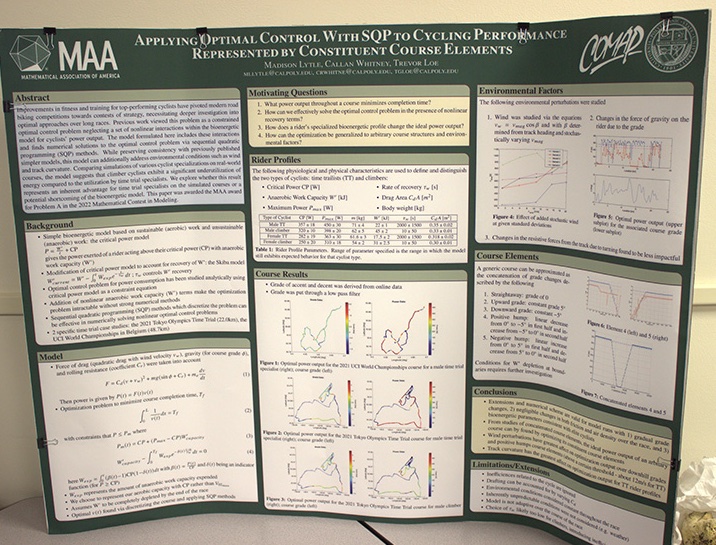America (MAA) for their outstanding submission, ranking in the Top 29 of approximately 15,000 teams that participated in the competition overall.

The Cal Poly team competed in a real-world modeling challenge among MAA college-level peers from across the U.S. and a host of other countries (the other top-ranking teams in their category were from China).

 

The Cal Poly math competition team displays their poster at the Fall Math Symposium.

 

Not only was the Cal Poly group’s submission a finalist, a level only 2% of submissions achieved, but their report was chosen by the MAA as the best submission for their problem.

 “Their work demonstrated creativity and a deep understanding of the modeling process via their formulation, implementation and analysis of a mathematical model that addressed the given contest question.”

Camp noted that in the year 2000 when a Cal Poly team won an award for an outstanding entry, the competition had 496 teams overall, signifying the elevated competitiveness of the event now.

To determine the optimal energy output of a professional cyclist, the Cal Poly student team considered several variables such as human biology (anaerobic biology), uphill versus downhill grades, drag, and race-track conditions such as curvature and course topography.  

Modern power monitoring systems can be mounted on a bike allow riders to track their power output during the race and make informed adjustments about improving pacing.  

The group’s analysis laid out formulas, models and conclusions about optimal cycling power output to accomplish the fastest possible results in professional races.  

“Madison and I are both are into a lot of applied math work going on at Cal Poly,” said Loe, a double major in physics. “We were able to get a sense of what using the math that we’ve learned feels like.” 

Because of variables such as a cyclist’s biological makeup and ability to store energy, along with course conditions such as hills and headwinds, they used sequential quadratic programming (SQP), a mathematical method used to solve a sequence of optimization subproblems, to generate numerical solutions.   

They proposed a method of optimizing cycling power output over subsections of tracks, called course elements, that may be concatenated (linked in a chain or series) into complex tracks. 

“Whatever parameters you use to represent the rider’s specific biology, there are certain interactions that are nonlinear,” said Lytle, a double major in aerospace engineering. “And that basically just makes them a lot more difficult to optimize and deal with numerically.” 

The study involved assessments of three tracks — the Tokyo Olympic Time Trial course, the UCI World Championships in Belgium and a constructed square course consisting of four rises and falls with a mathematically imposed radius of curvature of 10 meters around each bend. 

“The objective was not necessarily the model output, but the fact that the model is going to work,” Lytle said. “That’s so we can take into account these anaerobic effects because we can implement them in the model.” 

Among their conclusions:  

 

• the optimal strategy involves operating close to max power above one’s critical power (or highest average power you can sustain) during steep inclines, and dropping power output down as much as possible during downhills to recover  
• for courses with more variation in grade, model outputs recommend operating more reactively to the course features; alternatively, a flatter course prompts a pace which stays close to critical power at all times 
• due consideration should be taken into the environmental “perturbations” of the course, chiefly a strong headwind and the locations of sharp turns. If a headwind is greater than 15 meters per second, model outputs indicate that changing power output reactively to the wind, rather than staying consistent, will lower track times. 

 

The students were not allowed any faculty guidance during the competition.  

“Surprisingly, some of my physics classes were really helpful for some of the math, specifically optimization, which some physics classes, especially like classical mechanics, use,” Loe said. 

Lytle echoed her teammates assessment that skill sets in multiple disciplines helped.   

“Trevor and I are both double majors and Callan is an aerospace engineering major,” Lytle said. “We’ve learned a lot about drag in aerospace engineering classes.” 

Loe added: “With this competition, one of the hardest parts is deciding basically infinite things that you could account for and what to include and what to ignore. It was fun and a great experience to use math to solve a real-world problem.”